Tutorial
This page leads you through the main features of the applet.
The maps
The applet allows the iteration of a choice of two functions:
- Quadratic map: f(x)=a x (1-x) with 0 < a < 4
- Sine map: f(x)=(a/4) sin (
 x ) with
0 < a < 4
x ) with
0 < a < 4
The function is chosen from the list box at the bottom of the screen.
Choosing the function or hitting the Reset button brings up
the plot, and shows the first iteration from the starting value x0.
For now choose the default quadratic function.
The behavior depends on the value of a giving the "height" of the
function.
Fixed point
First try a=2.5 for the quadratic map by typing this value into the
a = box and
hitting Enter or Reset. The function is replotted for this value.
The iteration
can be done step by step by repeatedly hitting the Step button, or by
hitting the Start button, when the iteration is repeated with a speed
set by the Speed scroll bar (roughly in iterations per second). You
should see iterations approaching a fixed point at around x=0.6.
Period 2
Now change the value of a to a=3.1 and again iterate. Although
the values approach close to the fixed point value, which has moved to around
x=0.7,
rather than converging to this value the orbit moves away, and eventually
converges to an orbit that jumps between two values of x.
After watching this process a bit,
you can demonstrate the convergence to a period two orbit by restarting
the iteration after setting the value in the trans box to, say, 100
and hitting Enter or the Reset button -
this sets a number of iterations to be done to eliminate transient effects before
the first value is plotted.
Period 4 and higher
Increase a to a=3.5 and iterate: you will see a period 4
orbit. As a is slightly increased further (note the jumps we
have taken in a are becoming smaller) higher and higher period orbits
are found until at about a=3.57 a complex orbit with no apparent repetition
is obtained (try this!): this is the onset of chaos.
Functional composition
As the period of the orbit becomes higher, it is useful to look at a simpler
representation. We can do this by looking not at f(x) but at the
function f(f(x)). This is effectively looking at every second
iteration of f(x). We will use the notation f(2)(x)
for this. More generally we can look at f(m)(x) with
m=2nf, for example nf=2 gives
f(4)(x)=f(f(f(f(x)))) - now
you see the need for the new notation! Note, of course, that
f(2)
is not the square of the function f. You can study
f(m)
with m=2nf by setting the value in the nf box.
For example, first reset a to the value a=3.5 (remember this gave a
period 4 orbit). Now set nf to the value nf=1
(remember to hit Enter or Reset).
The function f(f(x)) is plotted, and can be iterated in the usual way.
Since this corresponds to "strobing" the orbit with period 2, the period 4
orbit in f appears as a period 2 orbit in f(2).
Rescaling
Since the orbit of f(2) is confined to a small region
near x=0.5 (at least for the default value of the initial condition
x0=0.35), it is convenient to "blow up" this central region. This is
done by the rescaling parameter nsc: both x and f around
0.5 are
rescaled by (- )nsc
with
)nsc
with  = 2.502807876... and then plotted between 0 and 1.
(The reason for using this scale factor will become apparent later.) The minus
sign inverts the curve for odd nsc as well.
Setting nsc=1 for a=3.5
and nf=1 will show just the enlarged central region - which (iterate)
actually
looks quite similar to the original period 2 orbit at a=3.1. This is the
beginning of the "scaling similarity" that is investigated further later.
(To make the picture look even nicer, you can slightly adjust the rescaling
further using the parameter scale, which simply rescales x and
f by this additional factor, e.g. set scale=1.08 so that the
intersection of the parabola and the diagonal line just fits in the plot region.
= 2.502807876... and then plotted between 0 and 1.
(The reason for using this scale factor will become apparent later.) The minus
sign inverts the curve for odd nsc as well.
Setting nsc=1 for a=3.5
and nf=1 will show just the enlarged central region - which (iterate)
actually
looks quite similar to the original period 2 orbit at a=3.1. This is the
beginning of the "scaling similarity" that is investigated further later.
(To make the picture look even nicer, you can slightly adjust the rescaling
further using the parameter scale, which simply rescales x and
f by this additional factor, e.g. set scale=1.08 so that the
intersection of the parabola and the diagonal line just fits in the plot region.
Geometric convergence
It turns out to be useful to look at a sequence of values of a,
a0 , a1 .... given by
am = ac - C 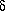 -m
where ac depends on the map function
(ac=3.56995... for the quadratic map), but
-m
where ac depends on the map function
(ac=3.56995... for the quadratic map), but 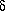 = 4.6692016091...
for all map functions. Such a
parameter that is
independent of the details of the map is known as a
universal parameter. The value of m can be used to
step through values of a yielding 2m orbits
(the symbol I in the list
box for m corresponds to infinity i.e. a=ac) The value of
C can be chosen
to give particular "types" of orbit: the applet has preset values for
the "superstable" orbit, where a is adjusted so that one point on the
orbit is at the maximum of the function, the "instability" point where the
2m just becomes unstable, and "bandmerging" values which
are useful to study the chaotic dynamics for a > ac. Study
this for both the quadratic and sine map, choosing successive values of m
and using nf and nsc to investigate
f 2nf rescaled.
= 4.6692016091...
for all map functions. Such a
parameter that is
independent of the details of the map is known as a
universal parameter. The value of m can be used to
step through values of a yielding 2m orbits
(the symbol I in the list
box for m corresponds to infinity i.e. a=ac) The value of
C can be chosen
to give particular "types" of orbit: the applet has preset values for
the "superstable" orbit, where a is adjusted so that one point on the
orbit is at the maximum of the function, the "instability" point where the
2m just becomes unstable, and "bandmerging" values which
are useful to study the chaotic dynamics for a > ac. Study
this for both the quadratic and sine map, choosing successive values of m
and using nf and nsc to investigate
f 2nf rescaled.
Putting it all together
Become familiar with the
appearance of the map itself at a=am i.e. (nf=nsc=0),
the 2m th
iterate of the map (nf=m, nsc=0) and other iterates, and the blown up
central portion
(nf=nsc=m).
[Return to Home Page]
[Table of Contents]
Last modified Thursday, September 26, 1996
Michael Cross
 x ) with
0 < a < 4
x ) with
0 < a < 4 x ) with
0 < a < 4
x ) with
0 < a < 4 )nsc
with
)nsc
with  = 2.502807876... and then plotted between 0 and 1.
(The reason for using this scale factor will become apparent later.) The minus
sign inverts the curve for odd nsc as well.
Setting nsc=1 for a=3.5
and nf=1 will show just the enlarged central region - which (iterate)
actually
looks quite similar to the original period 2 orbit at a=3.1. This is the
beginning of the "scaling similarity" that is investigated further later.
(To make the picture look even nicer, you can slightly adjust the rescaling
further using the parameter scale, which simply rescales x and
f by this additional factor, e.g. set scale=1.08 so that the
intersection of the parabola and the diagonal line just fits in the plot region.
= 2.502807876... and then plotted between 0 and 1.
(The reason for using this scale factor will become apparent later.) The minus
sign inverts the curve for odd nsc as well.
Setting nsc=1 for a=3.5
and nf=1 will show just the enlarged central region - which (iterate)
actually
looks quite similar to the original period 2 orbit at a=3.1. This is the
beginning of the "scaling similarity" that is investigated further later.
(To make the picture look even nicer, you can slightly adjust the rescaling
further using the parameter scale, which simply rescales x and
f by this additional factor, e.g. set scale=1.08 so that the
intersection of the parabola and the diagonal line just fits in the plot region.
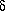 -m
-m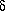 = 4.6692016091...
for all map functions. Such a
parameter that is
independent of the details of the map is known as a
universal parameter. The value of m can be used to
step through values of a yielding 2m orbits
(the symbol I in the list
box for m corresponds to infinity i.e. a=ac) The value of
C can be chosen
to give particular "types" of orbit: the applet has preset values for
the "superstable" orbit, where a is adjusted so that one point on the
orbit is at the maximum of the function, the "instability" point where the
2m just becomes unstable, and "bandmerging" values which
are useful to study the chaotic dynamics for a > ac. Study
this for both the quadratic and sine map, choosing successive values of m
and using nf and nsc to investigate
f 2nf rescaled.
= 4.6692016091...
for all map functions. Such a
parameter that is
independent of the details of the map is known as a
universal parameter. The value of m can be used to
step through values of a yielding 2m orbits
(the symbol I in the list
box for m corresponds to infinity i.e. a=ac) The value of
C can be chosen
to give particular "types" of orbit: the applet has preset values for
the "superstable" orbit, where a is adjusted so that one point on the
orbit is at the maximum of the function, the "instability" point where the
2m just becomes unstable, and "bandmerging" values which
are useful to study the chaotic dynamics for a > ac. Study
this for both the quadratic and sine map, choosing successive values of m
and using nf and nsc to investigate
f 2nf rescaled.