Scaling and Universality
Scaling of a
The demonstrations to this point should have illustrated the
following conclusion:
The map shows similar sorts of behavior
(instability, "superstable" cycle, band-merging etc.), except
involving the 2m cycle or band, at values of the
parameter a=am converging geometrically to a
"critical" value ac i.e.
am = ac +/- C 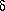 -m
-m
with 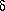 = 4.6692016091...
= 4.6692016091...
This sort of geometrical convergence is known as "scaling".
This is easy to show using the drop down boxes: set a value of
your choice for C in the text box, and vary m with the
drop-down list. The similarity of the behavior may be shown by
looking at the 2mth iterate (nf=m) and
blowing up the central region (nsc=m).
Another way of saying this is that if we take equivalent values of
a, that we call am, in successive
2m cycles, then the ratio
(am - am-1)/(am+1 -
am)
approaches a fixed value for large m. This asymptotic value
of the ratio is just 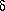 in the formula above.
in the formula above.
Other Scaling
Orbit splitting
The separation of points within the 2m cycles
also shows scaling. As we go from a 2 to a 4 to
8 .... the splitting of the orbit at successive transitions
becomes smaller and smaller. In fact at a=am the
splitting s scales as
sm = B  -m
-m
with
 = 2.502807876...
= 2.502807876...
(This is an oversimplification: the splitting actually depends on
which point around the orbit is considered - the quoted value is for
the point nearest the center x=0.5.) Another way of saying
this is
s(a) = B' |a - ac|b
with
b = log  /log
/log 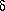 = 0.595...
= 0.595...
This puts the scaling in a form reminiscent of the scaling at a
thermodynamic phase transition.
The orbit splitting scaling has already been shown in the
demonstration, since the nsc parameter blows up the central
region by the amount  nsc.
nsc.
Lyapunov exponents, etc
There are many other scaling phenomena that cannot be demonstrated
with the present applet. For example the Lyapunov exponent
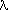 that determines the stability of the periodic orbits, or
sensitive dependence on initial
conditions in the chaotic state, scales at a=am
as
that determines the stability of the periodic orbits, or
sensitive dependence on initial
conditions in the chaotic state, scales at a=am
as
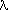 m = G 2 -m
m = G 2 -m
Again, this can be rephrased
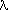 (a) = G' |a - ac|g
(a) = G' |a - ac|g
with
g=log 2/log 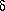 = 0.45...
= 0.45...
Universality
Even more amazing, the value of 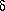 setting the geometric
convergence of am to ac is
universal, i.e. is independent of the form of the map (as long
as it falls into a broad family with the same sort of smooth maximum
as the quadratic map). The other scaling exponents
setting the geometric
convergence of am to ac is
universal, i.e. is independent of the form of the map (as long
as it falls into a broad family with the same sort of smooth maximum
as the quadratic map). The other scaling exponents
 , b,
and g are also universal. This remarkable fact means
that any system showing the onset of chaos by passing through
an infinite cascade of period doubling bifurcations will show the
same scaling with exactly the same numbers for these universal
quantities. We can therefore find the values by such different
schemes as iterating a one dimensional map on a computer, or by
measuring the properties of a fluid becoming chaotic by this route!
The universality has indeed been tested experimentally.
, b,
and g are also universal. This remarkable fact means
that any system showing the onset of chaos by passing through
an infinite cascade of period doubling bifurcations will show the
same scaling with exactly the same numbers for these universal
quantities. We can therefore find the values by such different
schemes as iterating a one dimensional map on a computer, or by
measuring the properties of a fluid becoming chaotic by this route!
The universality has indeed been tested experimentally.
You can crudely verify the universality here by changing to the
sine map in the drop down list, and observing the same set of
phenomena (geometric convergence, rescaling etc.).
Note that ac and the "amplitudes" A, B, B',
C, G, G' are not universal i.e. these numbers will be
different for different choices of map. Since these parameters set
the scale e.g. for x and are changed by simply redefining the
variable, it is not surprising they are not universal. It is
quantities that set ratios, such as the ratio is control
parameter differences (above) equal to 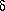 , that may be
universal. Some values of the nonuniversal quantities for the sine
map are set automatically when the sine function is chosen from the
drop down list.
, that may be
universal. Some values of the nonuniversal quantities for the sine
map are set automatically when the sine function is chosen from the
drop down list.
A small complication arising from the fact that
the rescaling amplitude B is not universal is that there may
be an overall scale factor (i.e. independent of m) when
"blowing" up the central portion to investigate different phenomena,
such as the periodic instability points, or the band merging points.
This is allowed for by using the parameter scale in the
applet. For example, for the quadratic map to view the:
- "superstable rescaled 1 cycles" i.e. Superstable and
"-" in the list boxes, a=am, nf=m,
nsc=n, use scale=0.88;
- "superstable rescaled 2 cycles" i.e. Superstable and
"-" in the list boxes, a=am,
nf=m-1, nsc=n-1, use scale=1.05;
- "instability of the rescaled 2m cycles",
i.e. Instability and "-" in the list boxes,
a=am, nf=m, nsc=n, use
scale=1.01;
- "bandmerging" for a > ac, i.e.
Bandmerging and "+" in the list boxes, and
a=am, nf=m, nsc=n, use
scale=1.14.
In all cases these values are chosen so that the rescaled map
curve and the diagonal intersect at the origin, and then the
iterations will remain within the (rescaled) unit box. For the sine
map, the values will be slightly different.
Last modified Saturday, September 7, 1996
Michael Cross
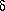 -m
-m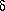 = 4.6692016091...
= 4.6692016091... -m
-m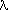 that determines the stability of the periodic orbits, or
that determines the stability of the periodic orbits, or