Chaos

This chapter describes some of the facts about the behavior of the maps for parameters for which the dynamics is chaotic.

To begin, restart the applet to return the parameters to their default values. You can eliminate transients by setting tr an to some high value e.g. tr an=200, and choose a fast Speed consistent with the speed of your computer (but see bugs).

Full band chaos

Set the parameter a to the maximum value a=4 consistent with iterated values remaining in the range 0< x <1, and start the iteration. Successive values of x_n appear quite "random", and the values eventually fill up the whole interval 0 < x < 1.

This chaotic motion can in fact be completely understood by making a transformation of variables. Define

x_n=sin²( z_n/2) The iteration of z for a=4 is then just z_n+1 = 2 z_n for 0 < z_n < 1/2
z_n+1 = 2 (1 - z_n) for 1/2 < z_n < 0 This is known as the tent map, and the dynamics is equivalent to an even simpler map: z_n+1 = 2 z_n mod 1 Successive values of z_n from a random initial value are as random as a coin toss (and in fact in binary representation answering the question of whether the n th value is to the right or left of 0.5 just gives the binary representation of the initial value, which is random for a random initial value).

Multi-band chaos

For other values of a the chaos is more complicated. In fact between the onset of chaos at a=a_c and the full band chaos at a=4 there are many different chaotic points interspersed with points giving periodic orbits of any period you want, each of which has its own period doubling cascade to chaos!

We can, however, find a sequence of values of a for which the chaos mimics, in reverse, the 2ⁿ cycle period doubling cascade.

For example set a=3.6 and iterate. Successive values of x appear "random" but there is also a definite pattern. Check that successive values of x always appear on opposite sides of the intersection of the diagonal with the curve. So there is a completely deterministic period-2 motion jumping backward and forward between two bands of values, with values spread "randomly" within the bands. This can be made clearer by looking at every second iterate setting nf=1. Now the x values appear on just one side of the intersection point. (Which side depends on the initial value: for x0=0.35 we get points on the lower side; setting e.g. x0=0.75, gives points on the greater side.)

As you probably expect by now, moving a down closer to a_c will give 4 chaotic bands, and then 8 bands, 16 ..... For example using values

a_m = a_c + 0.15 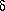delta

^-m (set with the boxes at the bottom of the screen) will give 2^m chaotic bands. Again you can check this by looking at the 2^mth iteration setting nf=m.

Band merging

The transition points at which the chaotic bands merge yield particularly simple chaotic dynamics. These band merging points can be set with the drop down boxes at the bottom of the screen. (Choose the "+" sign and "BandMerging".) Then for a_m = a_c + 0.485 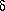delta

^-m the 2^m band just merge to give 2^m-1 bands. Within each of the 2^m bands the distribution of the chaos is exactly the same as the full band chaos at a=4. To show this set nf=m, and nsc=m to blow up the central portion making up one band, and compare with the full band chaos at a=4, nf=nsc=0.

[Return to Home Page]

Last modified 18 August, 2009
Michael Cross